La probabilidad no es cero
La probabilidad es el concepto más importante en la ciencia moderna, especialmente porque nadie sabe lo que significa. -Bertrand Russell
¿Puede algo imposible ser tan solo muy improbable? ¿Puede algo seguro ser en realidad un error? Sí y sí. Como aquella vez que mi hijo adolescente preguntó si podría estar embarazado.
No tanto; exagero. Después de una cita con su novia, platicó conmigo. El diálogo fue algo similar a esto aunque lo adorné para fingir inteligencia:
Él: Papá, ¿cuál es la probabilidad de que esté embarazado?
Yo: ¿Tú? ¿No tu novia? Cero (sin risas, sin burlas, sin mano en la cara). El embarazo solo...
Él: Pero... ¿cuántas veces nos has dicho que la probabilidad nunca es cero?
Yo: Mmm (uff). Bueno, si tuvieras cromosomas XX y un útero funcional no diagnosticados la probabilidad sería mayor que cero.1
Él: ¿Entonces, puedo estar embarazado?
Yo: No. ¿Puede un dado de seis lados marcados en orden caer en el número nueve?
Él: No, pero...
Yo: Aunque...
El: ¿Qué?
Yo: Nada, olvídalo. La probabilidad de que estés embarazado es prácticamente nula. Pero vamos a la farmacia, te quiero enseñar cómo la evidencia ajusta las probabilidades.
La probabilidad sí puede ser cero…
...En la probabilidad clásica. Ésta se basa en una idea muy simple y, según algunos expertos, elegante. Para que funcione, necesita cumplir con estas dos condiciones:
1. El número total de posibles resultados es finito y conocido.
2. Todos los resultados posibles tienen la misma probabilidad de ocurrir.2
Este modelo sirve a la perfección en sistemas cerrados y simples, como los juegos de azar. Volvamos al ejemplo del dado: si lanzamos uno de seis caras, ¿cuál es la probabilidad de sacar un 4?
P(Evento) = (Número de resultados favorables) / (Número total de resultados posibles)
P(Sacar un 4) = 1/6. Es decir: 16.67%.
¿Y de sacar un nueve? En un dado que visiblemente tiene seis caras marcadas del 1 al 6, la probabilidad es cero.
La diferencia entre lo imposible, lo de probabilidad cero y lo altamente improbable: que un dado de seis caras dé un 9 es imposible: no está en el espacio muestral. En cambio, elegir exactamente el número 0.5 al azar en el intervalo [0,1] tiene probabilidad cero, pero sí puede ocurrir.
El modelo clásico de la probabilidad es estático, depende de la frecuencia y no tiene mecanismos para incorporar el conocimiento previo. Necesitaremos un modelo donde el mundo sea un mapa dinámico que podemos actualizar. Thomas Bayes ha entrado al chat.
Bayes
Imagina que estás volviendo a casa y descubres que un accidente bloquea tu ruta habitual. ¿Qué haces? Cambias de camino: actualizas tu mapa con la nueva evidencia.
Se trata del pensamiento bayesiano. Asignamos probabilidades a nuestras creencias y las ajustamos cada vez que aparece información relevante. En pocas palabras: Teorema de Bayes = actualizar creencias con nueva evidencia.
La manera de cuantificar la incertidumbre:
Hay una persona sospechosa merodeando afuera de mi casa. ¿Qué tan peligrosa es?
Tu creencia inicial (la mayoría de la gente no roba) se ajusta con cada gesto sospechoso: capucha levantada y cara escondida ➜ más peligro; un camión de reparto estacionado en frente ➜ menos peligro.
Los investigadores diseñan experimentos científicos buscando evidencias que multipliquen la credibilidad de sus hipótesis, o divisores demoledores que las falseen. Los apostadores más hábiles afinan sus modelos y sus apuestas con cada punto ganado, con cada mueca observada en el rostro de los jugadores.
Cuantificar la evidencia y actualizar la creencia. Nada más… ¡y nada menos!
¡Nueva evidencia!
Yo: Esta es una prueba de embarazo, ¿ves? Orinas aquí encima, en la punta. Luego esperas dos minutos y lo traes.
Él: Qué raro eres, papá.
[Minutos después]
Yo: ¿Ah, mira… estas dos franjas color rosa aquí, ves? Una franja significa negativo y dos franjas es po… hazte para allá, déjame leer.
Él: Papá, no, tengo miedo. 😱
Ahora imaginemos que, para darle una lección de ciencia a mi hijo, lo llevé a comprar una prueba de embarazo y… ¿salió positivo! Porque en esta versión de los hechos la prueba dio positivo.
En la versión honesta, hubiera intentado tranquilizarnos repitiendo “es imposible” una y otra vez. En esta versión ideal, lo tranquilicé usando tres conceptos: el falso positivo, y las probabilidades o creencias a priori y a posteriori.
Un falso positivo ocurre cuando una prueba indica embarazo en una persona que no está embarazada. Puede tener diferentes causas (medicamentos en uso o errores del usuario al realizar o interpretar la prueba) y su tasa de probabilidad en estas pruebas suele encontrarse entre 0.1% y 1%.
Las probabilidades a priori son nuestras creencias iniciales. ¿Qué probabilidad le damos a algo antes de observar la evidencia?
Las probabilidades a posteriori son nuestras creencias actualizadas después de ver la evidencia.
¿Y la evidencia? Puede ser mil y una cosas: los resultados de un examen o del partido de tenis o de nuestros intentos de hacer amigos o de cuando comimos más de la cuenta y nos empachamos. Todo el día, todos los días, nuestro cerebro procesa nuevas evidencias para actualizar nuestras creencias.
El teorema de Bayes
P: La probabilidad.3
Para imaginar qué tan improbable es este embarazo, piénsalo así: si buscas un solo grano específico, de oro, en la inmensidad del desierto del Sahara (creencia inicial bajísima) y tu detector de metales suena en cuanto lo enciendes (nueva evidencia), ¿qué es más probable? ¿Que hayas encontrado ese grano exacto, o que tu detector sonó por error?
Mi creencia inicial del embarazo era casi cero. En el mundo real y con el conocimiento actual sobre fisiología humana, esta probabilidad es increíblemente baja.
La probabilidad de un falso positivo es casi incomparablemente mayor que la probabilidad de que un hombre se encuentre embarazado.
La probabilidad o creencia a posteriori, tras la prueba positiva, permanece cercana a cero pero dada la sorpresa merece atención. Ya sea una segunda prueba o una consulta médica, que ofrecerán nueva evidencia.
Creencia inicial: Digamos, cien millones en uno, 0.00000001%.
Creencia actualizada: Poco más de un millón en uno, 0.000099%. Abrumadoramente más probable que se trate de un falso positivo, que es un caso entre cien en un subgrupo de mujeres.
En conclusión, una prueba de embarazo positiva no confirmó la hipótesis de embarazo. ¿Por qué?4
Todos tienen derecho a sus propias creencias, pero nadie tiene derecho a sus propias verosimilitudes. -Sean Carroll
Vivir mejor
Cada evento que observas y cada dato que aprendes es evidencia. Piensa bayesiano.
Si encuentras evidencia nueva y relevante intégrala a tu modelo del mundo y actualiza tus verosimilitudes. Notarás, con el tiempo, una reducción en las sorpresas negativas que trae consigo la vida.
Tu cerebro ya está acostumbrado a procesar información; da un paso más y hazlo de forma consciente. Hará tu vida más fácil.
Cuando vayas a invertir tu dinero, Bayes.
Cuando vayas a interpretar las noticias del día, Bayes.
Cuando vayas a buscar un objeto perdido, Bayes.
Casi nunca sabremos la probabilidad absoluta de algo. Ayuda tener humildad. Pocas cosas son peores para la mente que estar totalmente seguro de un resultado y luego fallar de manera rotunda. Así surgen actitudes como la timidez, el autodesprecio o hasta el narcisismo.
Confirmar una creencia no es la mejor forma de aprender. Desmentir es mucho más poderoso que confirmar.
Bayes es un atajo de tu mente a la de los otros. Cuántas discusiones acabarían diferente si ambas partes lo aplicaran. Cuántas manos reprimirían la bofetada.
Cuando cambia la evidencia, cambia la probabilidad… y tal vez tu decisión.
Descargo de responsabilidad: No, nunca fuimos a comprar una prueba de embarazo para mi hijo. Ya teníamos otra evidencia previa, la más fuerte de todas para negar un embarazo: La cita con la novia no incluyó sexo. Que otra persona calcule la probabilidad de embarazarse así porque está más allá de mi imaginación.5
Gracias por permitir que nuestros textos se conviertan en evidencia nueva. ¿Tienes alguna anécdota sobre las probabilidades? ¡Nos encantaría leerla!
Tus comentarios nos motivan y, hasta ahora, hemos respondido a todos. Ya sea una anécdota, una pregunta, una sugerencia o una evidencia de nuestros errores, queremos leerte.
Existen casos documentados de gestación en individuos 46 XY y DSD (diferencias o desórdenes del desarrollo sexual), como el síndrome de Swyer.
Es decir, son equiprobables.
La teoría formal de la probabilidad se fundamenta en la axiomatización de Kolmogorov (Grundbegriffe der Wahrscheinlichkeitsrechnung, 1933), que introduce el concepto de una función P (probabilidad) con propiedades específicas.
La filosofía de la ciencia discute, hasta hoy y con fervor, una pregunta fundamental: ¿qué es P? Las interpretaciones de P abordadas en este texto son dos de las más importantes, aunque no las únicas: la interpretación clásica y la interpretación subjetiva o bayesiana. Los principales autores asociados a estas interpretaciones son Laplace y Bayes. También existen otras interpretaciones, como las que modelan sistemas estocásticos o aleatorios, así como las formalistas.
Existe una paradoja del falso positivo donde la intuición de la persona promedio falla. En los casos de eventos infrecuentes, como el cáncer de mama, puede ocurrir la falacia de la frecuencia base.
Este texto se nutrió de varias fuentes:
“High-speed intro to Bayes's rule”, Eliezer Yudkowsky.
Bayes theorem, the geometry of changing beliefs, 3Blue1Brown.
“Bayes for Everyone”, Scott Alexander.
Branden Fitelson, filósofo de la ciencia, en Mindscape 315: 27:48 a 40:30.
La cita de Sean Carroll proviene de su libro The Big Picture (2016). La de Bertrand Russell, de conferencia de 1929, citada por E.T. Bell en su libro The Development of Mathematics (1945).







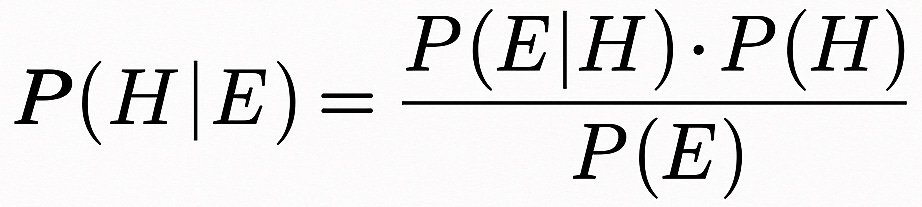

Frequentist meets Bayes, solo por el placer de debatir.
*Teóricamente, hay una probabilidad de que las moléculas aire de una casa se queden en la cocina, mientras nosotros vemos la tele en el salón, asfixiándonos así. ¿Ha sucedido esto alguna vez? ¿Sucederá algún día?
*Si no conozco el prior, ¿cuál es la calidad de mi estimación actualizada?
P.D.: en realidad soy muy fan de Bayes. 🙏😊
Mientras leía, me vinieron a la mente un par de ideas que quizá ya tienes presentes ,o incluso tenías tácitamente en el texto, pero que por experiencia creo que vale la pena hacer explícitas. Son distinciones que, aunque sutiles, no siempre están del todo claras para muchas personas, y tienden a confundirse incluso en discusiones bien intencionadas.
Una es la diferencia entre lo imposible, lo de probabilidad cero y lo altamente improbable. Por ejemplo, que un dado de seis caras dé un 9 es imposible: no está en el espacio muestral. En cambio, elegir exactamente el número 0.5 al azar en el intervalo [0,1] tiene probabilidad cero, pero sí puede ocurrir. Son cosas distintas, aunque en el lenguaje cotidiano las mezclemos con facilidad.
Pensé también en cómo el pensamiento bayesiano no nos obliga a aceptar cualquier evidencia como válida, sino a revisarla críticamente. Si algo que parecía imposible da una señal positiva, la pregunta no es solo “¿y si ocurre?”, sino también “¿cuál es la calidad de esta señal?”. Esa actitud de ajustar, sin abandonar el modelo de base a la primera, me parece esencial.
Gracias por abrir estos temas con claridad, ironía y ligereza —porque son justo los que más se benefician de ser pensados sin solemnidad.
Un gusto leerte,
—J. Rogelio